Fast Marching Segmentation

Overview

The fast marching method is a simple form of level-set evolution where only a positive speed term is used to govern the differential equation. The resulting level-set contour only grows over time. Practically, this algorithm can be used as an advanced region growing segmentation which is controlled by a speed image.

A good propagation speed image for segmentation is close to zero near object boundaries and relatively high in between. In this example, an input feature image is smoothed with an anisotropic diffusion method, then the gradient magnitude is used to produce an edge image. A Gaussian with a parameterized sigma is used during the gradient computation to enable the level-set to slow down near edges. The Sigmoid filter performs a linear transform on the gradient magnitude so that boundaries are near zero and homogeneous regions are close to one. The values for alpha and beta are provided in the testing code. The heuristics used to estimate good values are dependent on the minimum value along a boundary and the mean value of the gradient in the object’s region.

Lastly the fast marching filter is configured with an initial trial point and starting value. Each trial point consists of a tuple for an image index including an optional unsigned starting seed value at the trial point. The trial points are the starting location of the level-set. The output of the fast marching filter is a time-crossing map that indicate the time of arrival of the propagated level-set front. We threshold the result to the region the level-set front propagated through to form the segmented object. A graphical interface can be constructed to show the contour propagation over time, enabling a user to select a the desired segmentation.

Example Run

Running the Python code with the following inputs:

main('BrainProtonDensitySlice.png', 'fastMarchingOutput.mha', 81 114 1.0 -0.5 3.0 100 110)

produces the input & output images below.

Input/Output Images

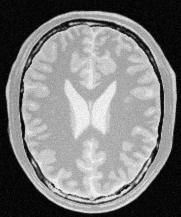
Input Image

Speed Image

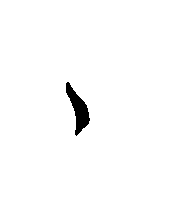
Time Crossing Map

Final Segmentation

Code

C#C++Python

// This example is based on ITK's FastMarchingImageFilter.cxx example

//INPUTS:  {BrainProtonDensitySlice.png}
//    OUTPUTS: {FastMarchingImageFilterOutput5.png}
//    ARGUMENTS:    81 114 1.0  -0.5  3.0   100 100


using System;

using SitkImage = itk.simple.Image;
using System.Globalization;

namespace itk.simple.examples
{
    public class FastMarchingSegmentation
    {
        static void Main(string[] args)
        {
            if (args.Length < 9)
            {
                Console.WriteLine("Missing Parameters ");
                Console.WriteLine("Usage: " + System.AppDomain.CurrentDomain.FriendlyName +
                                  " inputImage outputImage seedX seedY " +
                                  " Sigma SigmoidAlpha SigmoidBeta TimeThreshold");
                return;
            }

            string inputFilename = args[0];
            string outputFilename = args[1];

            uint[] seedPosition = { Convert.ToUInt32(args[2]), Convert.ToUInt32(args[3]),0 };

            double sigma = double.Parse(args[4], CultureInfo.InvariantCulture);
            double alpha = double.Parse(args[5], CultureInfo.InvariantCulture); ;
            double beta = double.Parse(args[6], CultureInfo.InvariantCulture);
            double timeThreshold = double.Parse(args[7], CultureInfo.InvariantCulture);
            double stoppingTime = double.Parse(args[8], CultureInfo.InvariantCulture);

            // Read input image

            SitkImage inputImage = SimpleITK.ReadImage(inputFilename, PixelIDValueEnum.sitkFloat32);

            //  The input image will be processed with a few iterations of
            //  feature-preserving diffusion.  We create a filter and set the
            //  appropriate parameters.

            CurvatureAnisotropicDiffusionImageFilter smoothing = new CurvatureAnisotropicDiffusionImageFilter();
            smoothing.SetTimeStep(0.125);
            smoothing.SetNumberOfIterations(5);
            smoothing.SetConductanceParameter(9.0);
            SitkImage smoothingOutput = smoothing.Execute(inputImage);

            SitkImage gradientMagnitudeOutput = SimpleITK.GradientMagnitudeRecursiveGaussian(smoothingOutput, sigma);

            SitkImage sigmoidOutput = SimpleITK.Sigmoid(gradientMagnitudeOutput, alpha, beta, 1.0, 0.0);


            FastMarchingImageFilter fastMarching = new FastMarchingImageFilter();

            //VectorUIntList trialPoints; Add trialPoints into list if using multiple seeds. Here we only use one seedpoint

            VectorUInt32 trialPoint = new VectorUInt32(3);
            trialPoint.Add(seedPosition[0]);
            trialPoint.Add(seedPosition[1]);
            trialPoint.Add(seedPosition[2]);

            fastMarching.AddTrialPoint(trialPoint);

            //  Since the front representing the contour will propagate continuously
            //  over time, it is desirable to stop the process once a certain time has
            //  been reached. This allows us to save computation time under the
            //  assumption that the region of interest has already been computed. The
            //  value for stopping the process is defined with the method
            //  SetStoppingValue(). In principle, the stopping value should be a
            //  little bit higher than the threshold value.

            fastMarching.SetStoppingValue(stoppingTime);

            SitkImage fastmarchingOutput = fastMarching.Execute(sigmoidOutput);

            BinaryThresholdImageFilter thresholder = new BinaryThresholdImageFilter();
            thresholder.SetLowerThreshold(0.0);
            thresholder.SetUpperThreshold(timeThreshold);
            thresholder.SetOutsideValue(0);
            thresholder.SetInsideValue(255);
            SitkImage result = thresholder.Execute(fastmarchingOutput);

            SimpleITK.WriteImage(result, outputFilename);

        }
    }
}